Random system generator
Read Generator Engine Utilities
before reading the geneator algorithm.
In order to generate a random lmp system (of finite state space), we need to
know at least the following parameters :
- the X set formed of several disjoints intervals that represents the
starting states for which a transition exists.
- the Y set formed of several disjoints intervals that represents the ending
states of a transition.
- the state space representing all the system states. X and Y must all be a
subset of the state space.
- the actions usable by the transitions
- the expressions attached to the transitions
In order to generate these parameters, the following values will be used :
- the number of intervals included in X and Y
- the number of actions to generate
- the number of transitions per interval x from X
- the number of action per interval x from X
- the probability of innectiveness of an action
Note that the closer the number of transitions per interval will be of
the number of intervals, the more connected the system will be. If those two
numbers are equal, then the system will be completely connected. All the five
parameters are set using the RandomizedModel class.
In order to enhance the performances of the random system generator and use
as little memory as possible, we will directly write each transition to the
disk. The only problematic during transition generation is that according to LMP
constraints :
1. if two transition start from the same x set to reach the same y set using the
same action, then these transitions are the same.
2. the sum of all maximum probabilities for each transition for an action and a
starting state set must never be greater than 1.
Fortunately, in order to satisfy these two restriction, knowledge of the entire
system is not necessary. In fact, there is no need to keep a transition list as
these can be generated directly to the disk, by only knowing the sum of the
probabilities and the visited state sets from Y for a x set of state and an
action a.
The function BAGOF in this code selects a certain number of actions from the
A set.
GENERATESYSTEM
(Part 1: Generating the state space, and the X and Y sets)
(Choosing the number of intervals in X and Y)
n 
random(|X|)
states [0, k1
* n]
(Generating the X and Y sets)
(Partitionning the state space length)
lengthsX
PARTITION(length of states,n)
lengthsY
PARTITION(length of states,n)
(These variables shall determine the lower bound value of the
interval and its inclusion state)
boundX
0 (the state space starts at zero)
boundY
0
includedX
false (the first bound is always included)
includedY false
FOR i
ß1 TO n
X[i]
[boundX,
boundX + lengthsX[i] ]
Y[i]
[boundY,
boundY + lengthsY[i] ]
X[i]inclusiveLeft
¬includedX(intervals
are disjoints)
Y[i]inclusiveLeft
¬includedY
(choosing a new value for incudedX and includedY)
includedX random(
{true, false} )
includedY random(
{true, false} )
X[i]inclusiveRight
includedX
Y[i]inclusiveRight
includedY
(incrementing bounds)
boundX boundX
+ lengthsX[i]
boundY boundY
+ lengthsY[i]
END FOR
(The lower bound is inclusive to the right)
X[i]inclusiveRight
true
Y[i]inclusiveRight
true
(Part 2: Generating the action set)
(We shall determine the number of actions to generate in the A set)
a
random(|A|)
FOR
i
1
TO a
A[i] ”action”+i
(a generic name is given)
FIN FOR
(Partie 3 : Generating the transitions)
(We shall create the transitions for each x in the X set)
FOR i 1
TO length of X
(We shall determine the number of transitions for this x)
nbTrans
random(|T|/|X|)
(We shall determine the number of actions for whis transition)
nbActions random(|A|/|X|)
(Selecting actions from the A set for which we will generate
transitions)
actions BAGOF(A,
nbActions)
(We will partition the number of transitions for each action)
nbTransAction PARTITIONINTEGER(nbTrans,
nbActions)
(Each chosen action will generate transitions)
FOR j 1
TO nbActions
(Determining the overall maximum probability of this action)
q 1-random(P)
(Partitionning the probabilities)
Q PARTITION(q,
nbTransAction[j] )
(We must never create two transition with the same y)
Yvisited
nil
(Generating each transition)
FOR k 1
TO nbTransAction[j]
(Selecting y)
y random(Y
– Yvisited)
(Creating the transition)
t TRANSITION(X[i],
y, actions[j], Q[k])
END
FOR j
END FOR i
END
OF generatesystem
The use of partition on Q ensures that the system will
never break the LMP constraints.
Generating a transition
To succesfully generate a transition,
five parameters need to be known :
- the starting state set x
- the ending state set y
- the triggered action
- the maximum probability
To avoid violating the LMP constraints,
we shall generate functions that start from a [0,1] interval of states to reach
a [0,1] interval of ending states. We will then adjust this function to the x
and y, following these formulae :
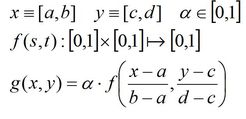
Five functions can be generated :
Constant :
This function does not take the value of
x into account. It is equivalent to x being a discrete interval.
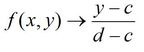
Uniform :
All the
states included in the x set have the same probability of being chosen.
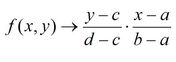
Exponential :
As this function requires a lambda
parameter, we will choose one between 1 and 10 to introduce variations in the
system.
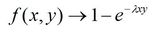
Normal :
Based on a
reduced centered normal law density function :
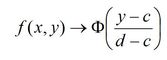
Logarithmic :
This is an
adaptation of the classic normal law. Unfortunately, only the y set will be
taken into account since the formula would become too long if the x and y set
were both to be included.
(Adaptation from :
http://mathworld.wolfram.com/LogarithmicDistribution.html)
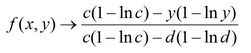
Here is the
algorithm :
TRANSITION(x, y, action, α)
(Choosing a function)
r random(F
– Fexclues)
(Computing parameters)
a borne inférieure de x
b borne supérieure de x
c borne inférieure de y
d borne inférieure de y
(The functions are generated in a string recognizable by the
JavaMath library used in Cismo.)
f generating the function
t créer transition(x,y,action,f)
(Writing transition on disk and freeing the transition from memory)
WRITE t
FREE t
END of transition
Data package, Generator package,
Logic Package,
Engine